Se tudo correr bem já todos pararam de ler por aqui.
Agora observem o grafico típico de uma parábola, de função x quadrado:
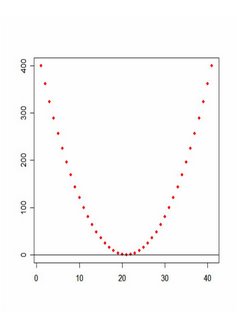
Este é o modelo matemático para o clássico "bater no fundo". A curva desce a pique, acalma um pouco no final, bate no fundo e, ultrapassado o ponto de inflexão, recupera, primeiro lentamente e depois mais depressa, até voltar ao topo. A boa notícia aqui é que tudo o que desce sobe.
Depois à outra hipótese, outra curva que tem algumas semelhanças, mas uma grande diferença. Observem o gráfico da função x ao cubo:

O que aqui acontece é que atingido o "fundo", a curva desacelera, parece até estabilizar no "fundo", só para depois acelerar vertiginosamente na direcção do que está para lá do fundo, algo a que um matemático chamaria tender para menos infinito!
Neste segundo caso não existe um ponto de inflexão, é mais estilo "Highway to Hell" ao som dos riffs roufenhos e agressivos dos AC/DC.
Substituam os pontos dos gráficos pelo nosso estado de espírito em cada dia e depois venham cá dizer se a matemática não se aplica à vida! Ás vezes o que precisamos é de pontos de inflexão, antes que o x ao cubo tome conta de nós...
And the Oscar for the most demented post goes to... ME!
4 comentários:
já vi posts piores. até é bastante razoável e coerente.
Parabéns! Nunca vi a minha vida tão bem explicada!
Já agora, impõe-se uma correcção: o segundo gráfico corresponde à função - (menos) x ao cubo!
Oscar muito bem atribuido!
Enviar um comentário